Riyaziyyatda cəmləmə (böyük yunan siqma simvolu ilə işarələnir) ədədlərin cəmləri toplusudur. Məbləğ nədir? Bu, belə bir hərəkətin nəticəsidir. Rəqəmlər soldan sağa bir-birinin ardınca əlavə edilərsə, aralıq nəticə qismən cəmidir.
Məbləğ nədir?
Cəmlənəcək ədədlər tam, rasional, real və ya mürəkkəb ola bilər. Onlara əlavə olaraq, digər növ dəyərlər də əlavə edilə bilər: vektorlar, matrislər, polinomlar və ümumiyyətlə hər hansı bir əlavə qrupun elementləri (və ya hətta monoid).
Şərtlərin elementlərinin sayı məhduddursa, o zaman toplama həmişə dəqiq müəyyən edilmiş qiymət verir. Sonsuz dəyərlər ardıcıllığının cəminə sıra deyilir. Onun dəyəri çox vaxt limitdən istifadə etməklə müəyyən edilə bilər (baxmayaraq ki, bəzən dəyər sonsuz ola bilər).
Ardıcıllıqlar
Radların cəmi [3, 7, 2, 1] dəyəri ona daxil edilmiş rəqəmlərin cəmi olan ifadə ilə müəyyən edilə bilər, məsələn, 3 + 7 + 2 + 1=13. əlavəassosiativ olaraq, cəmi şərtlərin necə qruplaşdırılmasından asılı deyil, məsələn, (3 + 7) + (2 + 1) və 3 + ((7 + 2) + 1) hər ikisi doqquza bərabərdir, buna görə də mötərizələr adətən ilə imtina etdi. Əlavə də kommutativdir, buna görə də şərtlərin yenidən təşkili cəminin dəyərini dəyişmir. Nəzərə alın ki, bu xüsusiyyət sonsuz toplama üçün işləməyə bilər.

Bu növ ardıcıllıqların cəmlənməsi üçün xüsusi qeyd yoxdur. İkidən az element varsa, yalnız kiçik bir nüans var. Bir üzvün ardıcıllığının cəmində üstəlik işarəsi yoxdur (rəqəmin özündən fərqlənmir) və heç bir element yoxdursa, o zaman hətta yazıla bilməz (lakin bunun əvəzinə onu işarələmək olar) onun dəyəri "0"). Bununla belə, ardıcıllığın şərtləri funksiya kimi xüsusi nümunə ilə müəyyən edilirsə, toplama operatoru faydalı və ya hətta vacib ola bilər.
Qeyd
Cəminin nə olduğunu başa düşmək üçün onun görünüşünü təhlil etmək də lazımdır.
1-dən 100-ə qədər tam ədədlər ardıcıllığını cəmləmək üçün tez-tez çatışmayan üzvləri göstərmək üçün ellipsdən ibarət ifadə istifadə olunur: 1 + 2 + 3 + 4 + … + 99 + 100. Nümunə belədir bu nümunədə görmək olduqca asandır. Bununla belə, daha mürəkkəb variantlar üçün elementlərin qiymətini tapmaq üçün istifadə olunan qaydanı dəqiq müəyyən etmək lazımdır ki, bu da "Σ" toplama operatorundan istifadə etməklə əldə edilə bilər. Bu simvoldan (siqma) istifadə edərək, aşağıdakı qeydi tətbiq edə bilərsiniz:
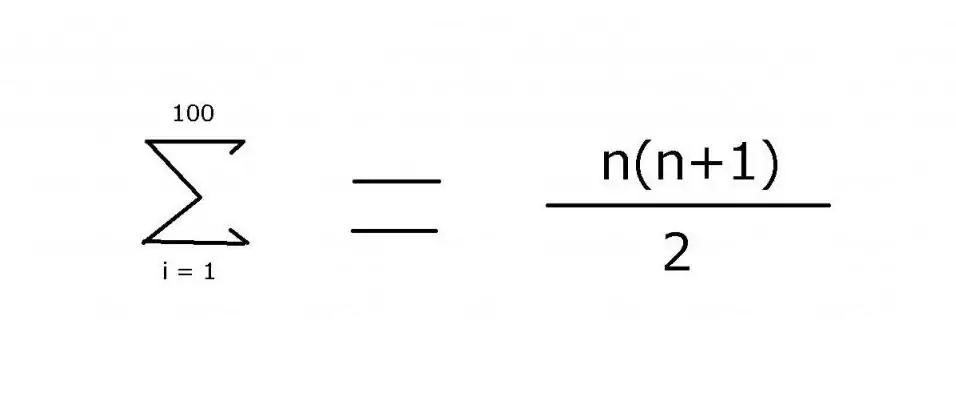
Bu ifadənin dəyəri 5050-dir. Onu düsturun ikinci hissəsinin gəldiyi yer olan riyazi induksiyadan istifadə etməklə tapmaq olar.
Fərqli ardıcıllıqlar üçün düstur dəyişəcək. Qeydiyyat prosesi bəzi sonsuz ardıcıllığın ilkin görüntüsünü axtarmağa və sonra onu düsturla təsvir etməyə qədər azaldılır. Bunu etdikdən sonra konkret halda məbləğin nə olduğunu başa düşmək çətin deyil.
Ədədlərin işarələri ilə (artı və ya mənfi) əlavə olunduğunu aydınlaşdırmaq lazım gəldikdə cəbri cəmi terminindən istifadə olunur. Məsələn, elektrik dövrələri nəzəriyyəsində Kirchhoffun dövrə qanunları bir nöqtədə birləşən keçiricilər şəbəkəsindəki cərəyanların cəbri cəmini nəzərə alır, bu da qovşaqdan daxil olan və çıxan cərəyanlara əks işarələr verir.






